what is the term used to describe an annuity with an infinite life?

4.3 Valuing a Serial of Cash Flows

Learning Objectives

1. Discuss the importance of the thought of the time value of money in fiscal decisions.
2. Define the present value of a series of greenbacks flows.
3. Define an annuity.
4. Place the factors you lot need to know to calculate the value of an annuity.
5. Discuss the relationships of those factors to the annuity's value.
6. Define a perpetuity.

It is quite common in finance to value a series of future cash flows (CF), perchance a series of withdrawals from a retirement business relationship, interest payments from a bond, or deposits for a savings account. The present value (PV) of the series of greenbacks flows is equal to the sum of the present value of each greenbacks menstruation, so valuation is straightforward: notice the present value of each greenbacks flow and then add them upward.

Ofttimes, the series of cash flows is such that each cash period has the aforementioned future value. When at that place are regular payments at regular intervals and each payment is the same amount, that series of cash flows is an annuityA serial of cash flows in which equal amounts happen at regular, periodic intervals. . Most consumer loan repayments are annuities, every bit are, typically, installment purchases, mortgages, retirement investments, savings plans, and retirement plan payouts. Fixed-rate bond interest payments are an annuity, as are stable stock dividends over long periods of time. Y'all could recollect of your paycheck every bit an annuity, every bit are many living expenses, such as groceries and utilities, for which you pay roughly the same amount regularly.

To calculate the present value of an annuity, you need to know

• the amount of the future cash flows (the aforementioned for each),
• the frequency of the cash flows,
• the number of cash flows (t),
• the rate at which time affects value (r).

Almost any computer and the many readily available software applications can practice the math for you, only it is of import for yous to sympathize the relationships between time, hazard, opportunity toll, and value.

If yous win the lottery, for example, you are typically offered a choice of payouts for your winnings: a lump sum or an annual payment over twenty years.

The lottery bureau would adopt that you took the almanac payment because it would not have to surrender every bit much liquidity all at in one case; it could hold on to its liquidity longer. To make the almanac payment more attractive for y'all—information technology isn't, considering yous would want to take more liquidity sooner—the lump-sum option is discounted to reflect the present value of the payment annuity. The discount rate, which determines that present value, is chosen at the discretion of the lottery bureau.

Say yous win $10 million. The lottery bureau offers you a option: have $500,000 per twelvemonth over 20 years or take a one-time lump-sum payout of $six,700,000. You would choose the culling with the greatest value. The present value of the lump-sum payout is $6,700,000. The value of the annuity is not simply $ten million, or $500,000 × 20, because those $500,000 payments are received over time and fourth dimension affects liquidity and thus value. So the question is, What is the annuity worth to you?

Your discount rate or opportunity cost volition make up one's mind the annuity's value to you, as Effigy four.8 "Lottery Present Value with Different Discount Rates" shows.

Effigy 4.8 Lottery Present Value with Dissimilar Discount Rates

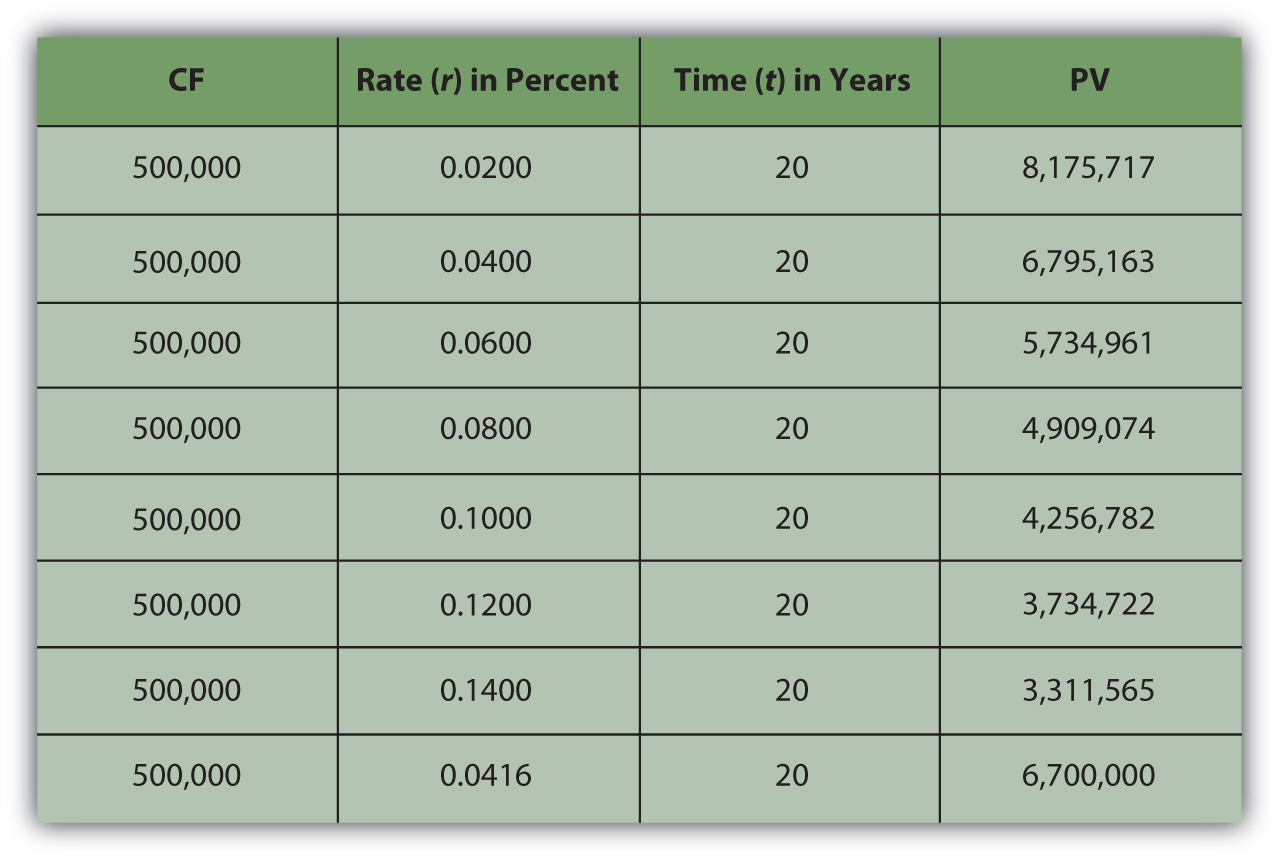
As expected, the present value of the annuity is less if your discount rate—or opportunity price or next best choice—is more. The annuity would be worth the same to you as the lump-sum payout if your discount rate were iv.16 percent.

In other words, if your discount rate is about 4 percent or less—if you don't have more than lucrative choices than earning 4 percent with that liquidity—then the annuity is worth more to you than the immediate payout. You lot can afford to wait for that liquidity and collect information technology over twenty years considering you have no better choice. On the other hand, if your discount rate is higher than 4 percentage, or if you feel that your use of that liquidity would earn you more than four percent, then you have more lucrative things to do with that coin and you want information technology at present: the annuity is worth less to you than the payout.

For an annuity, equally when relating one cash menstruum's present and future value, the greater the charge per unit at which fourth dimension affects value, the greater the effect on the present value. When opportunity cost or risk is low, waiting for liquidity doesn't matter as much as when opportunity costs or risks are college. When opportunity costs are low, you accept cypher better to exercise with your liquidity, merely when opportunity costs are college, you may sacrifice more than by having no liquidity. Liquidity is valuable because it allows you to make choices. After all, if there are no more than valuable choices to make, you lose little past giving up liquidity. The college the rate at which time affects value, the more information technology costs to wait for liquidity, and the more choices pass y'all by while you wait for liquidity.

When risk is low, it is not actually important to have your liquidity firmly in hand any sooner because you'll have information technology sooner or after anyway. But when chance is high, getting liquidity sooner becomes more important because it lessens the chance of not getting information technology at all. The college the rate at which time affects value, the more hazard at that place is in waiting for liquidity and the more hazard that you won't get it at all.

As r increases	the PV of the annuity decreases
Every bit r decreases	the PV of the annuity increases

You can also wait at the human relationship of time and cash flow to annuity value. Suppose your payout was more than (or less) each year, or suppose your payout happened over more (or fewer) years (Effigy iv.9 "Lottery Payout Present Values").

Figure 4.9 Lottery Payout Present Values

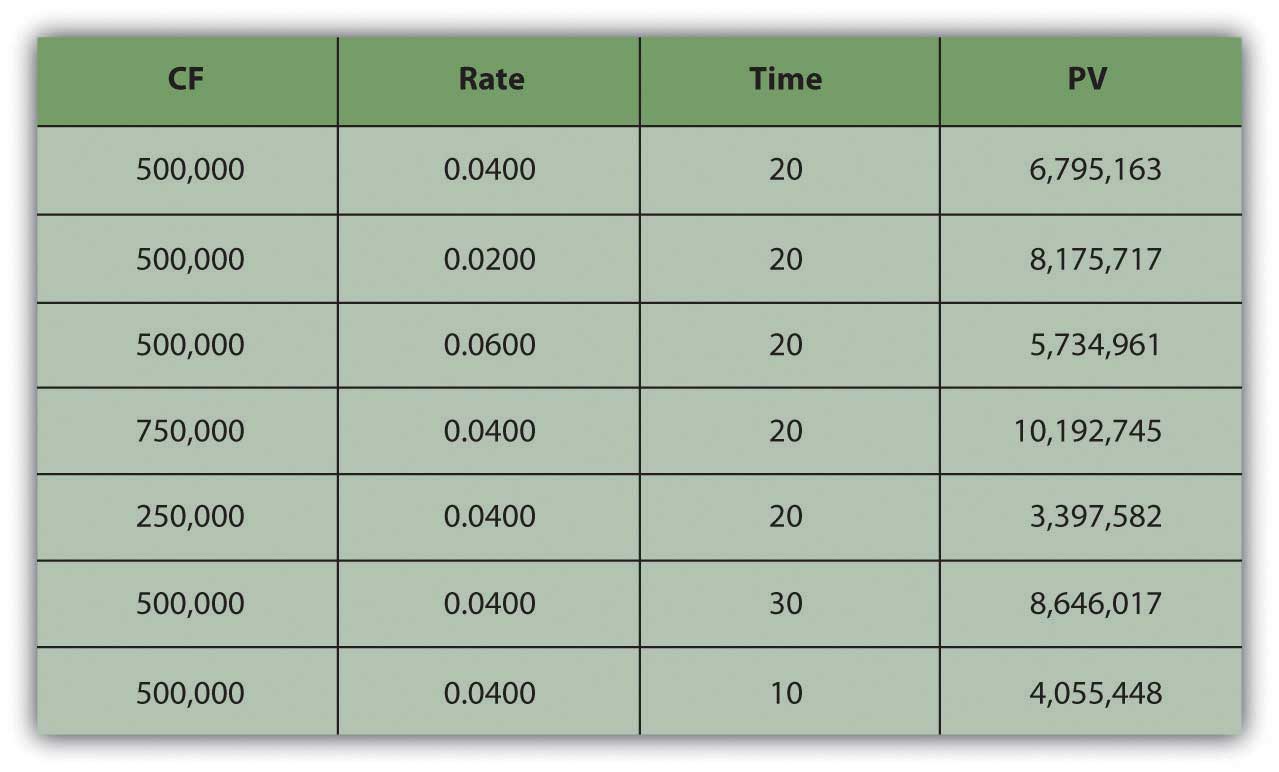
As seen in Figure 4.9 "Lottery Payout Present Values", the amount of each payment or greenbacks flow affects the value of the annuity because more greenbacks means more liquidity and greater value.

As CF increases	the PV of the annuity increases
Every bit CF decreases	the PV of the annuity decreases

Although fourth dimension increases the distance from liquidity, with an annuity, it too increases the number of payments because payments occur periodically. The more periods in the annuity, the more cash flows and the more liquidity in that location are, thus increasing the value of the annuity.

As t increases	the PV of the annuity increases
As t decreases	the PV of the annuity decreases

It is mutual in financial planning to calculate the FV of a series of greenbacks flows. This calculation is useful when saving for a goal where a specific amount will be required at a specific betoken in the future (eastward.yard., saving for college, a hymeneals, or retirement).

It turns out that the relationships between time, risk, opportunity cost, and value are anticipated going forward every bit well. Say you decide to take the $500,000 annual lottery payout for xx years. If you deposit that payout in a bank account earning 4 per centum, how much would y'all have in xx years? What if the account earned more interest? Less interest? What if you won more (or less) and so the payout was more than (or less) each twelvemonth?

What if you won $15 meg and the payout was $500,000 per twelvemonth for thirty years, how much would you accept and so? Or if you won $5 million and the payout was only for ten years? Effigy four.10 "Lottery Payout Future Values" shows how future values would modify.

Figure 4.10 Lottery Payout Futurity Values

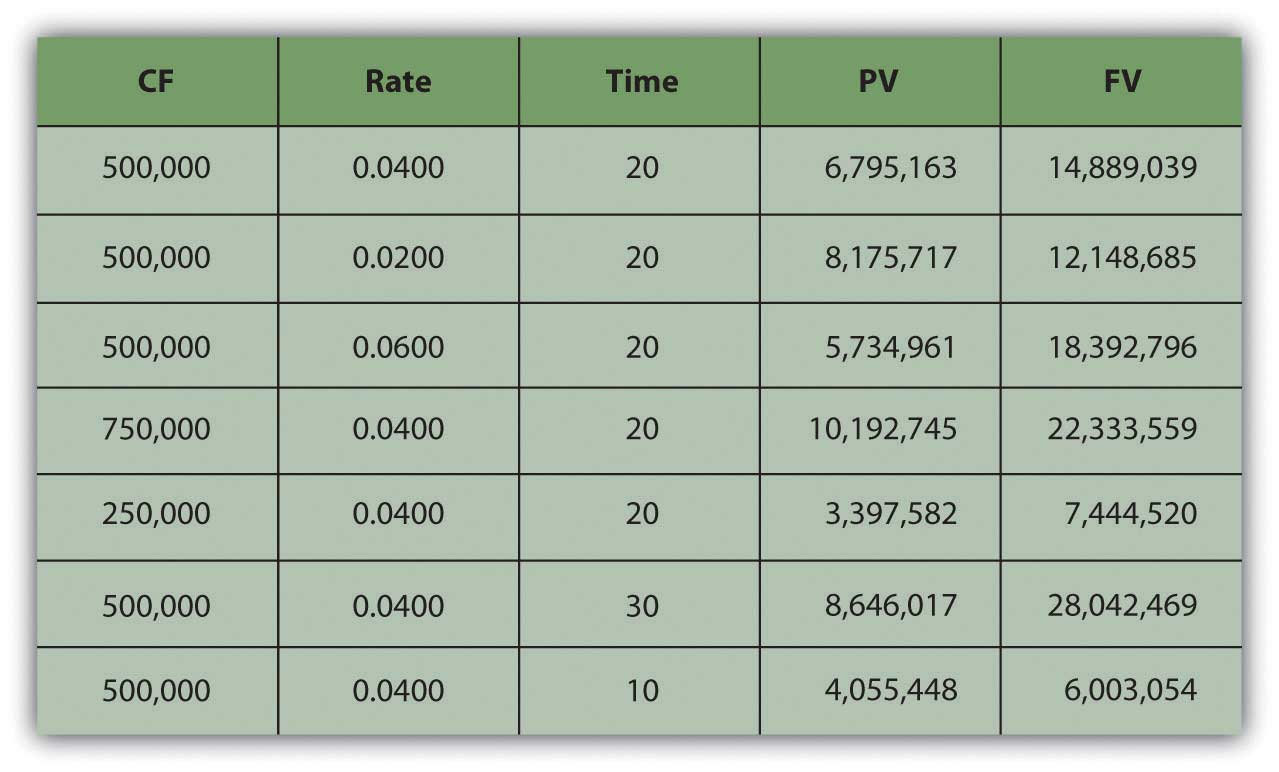
Going forwards, the rate at which time affects value (r) is the rate at which value grows, or the rate at which your value compounds. It is also called the charge per unit of compoundingThe effect of time on value or the charge per unit at which time affects value; used when calculating the equivalent future value of a nowadays amount of liquidity. . The bigger the event of time on value, the more than value you lot will end up with because more fourth dimension has affected the value of your coin while it was growing as information technology waited for you. And so, looking forward at the future value of an annuity:

As r increases	the FV of the annuity increases
Equally r decreases	the FV of the annuity decreases

The amount of each payment or cash catamenia affects the value of the annuity because more cash ways more liquidity and greater value. If yous were getting more cash each year and depositing it into your business relationship, y'all'd end up with more value.

Every bit CF increases	the FV of the annuity increases
As CF decreases	the FV of the annuity decreases

The more time there is, the more time tin affect value. As payments occur periodically, the more cash flows there are, the more liquidity there is. The more than periods in the annuity, the more cash flows, and the greater the effect of time, thus increasing the hereafter value of the annuity.

As t increases	the FV of the annuity increases
Equally t decreases	the FV of the annuity decreases

There is also a special kind of annuity chosen a perpetuityAn space annuity; a stream of periodic cash flows that continues indefinitely. , which is an annuity that goes on forever (i.e., a series of greenbacks flows of equal amounts occurring at regular intervals that never ends). Information technology is hard to imagine a stream of cash flows that never ends, but information technology is actually non so rare as information technology sounds. The dividends from a share of corporate stock are a perpetuity, considering in theory, a corporation has an space life (every bit a separate legal entity from its shareholders or owners) and because, for many reasons, corporations like to maintain a steady dividend for their shareholders.

The perpetuity represents the maximum value of the annuity, or the value of the annuity with the well-nigh cash flows and therefore the nearly liquidity and therefore the nigh value.

Life Is a Series of Cash Flows

Once you lot understand the idea of the fourth dimension value of money, and of its use for valuing a series of cash flows and of annuities in item, you tin can't believe how yous ever got through life without information technology. These are the cardinal relationships that structure so many financial decisions, most of which involve a series of cash inflows or outflows. Understanding these relationships can exist a tool to help you answer some of the nigh common fiscal questions most buying and selling liquidity, considering loans and investments are and so ofttimes structured as annuities and certainly take identify over time.

Loans are usually designed as annuities, with regular periodic payments that include interest expense and principal repayment. Using these relationships, you tin see the effect of a different amount borrowed (PV_annuity), interest rate (r), or term of the loan (t) on the periodic payment (CF).

For example, if you lot become a $250,000 (PV), thirty-year (t), 6.five percentage (r) mortgage, the monthly payment will be $1,577 (CF). If the aforementioned mortgage had an interest rate of only 5.five percent (r), your monthly payment would decrease to $1,423 (CF). If information technology were a fifteen-twelvemonth (t) mortgage, still at half-dozen.five percent (r), the monthly payment would be $2,175 (CF). If you can make a larger down payment and borrow less, say $200,000 (PV), then with a thirty-year (t), 6.5 pct (r) mortgage you monthly payment would exist simply $one,262 (CF) (Figure 4.eleven "Mortgage Calculations").

Effigy four.11 Mortgage Calculations

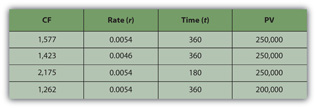
Note that in Figure 4.11 "Mortgage Calculations", the mortgage rate is the monthly rate, that is, the almanac rate divided past twelve (months in the yr) or r ÷ 12, and that t is stated equally the number of months, or the number of years × 12 (months in the year). That is because the mortgage requires monthly payments, and then all the variables must be expressed in units of months. In general, the periodic unit used is defined by the frequency of the cash flows and must agree for all variables. In this example, because y'all have monthly greenbacks flows, y'all must summate using the monthly discount rate (r) and the number of months (t).

Saving to reach a goal—to provide a downwardly payment on a house, or a child's instruction, or retirement income—is often accomplished by a plan of regular deposits to an account for that purpose. The savings program is an annuity, so these relationships can be used to calculate how much would have to exist saved each menses to accomplish the goal (CF), or given how much can be saved each menstruation, how long it will take to accomplish the goal (t), or how a ameliorate investment render (r) would affect the periodic savings, or the fourth dimension needed (t), or the goal (FV).

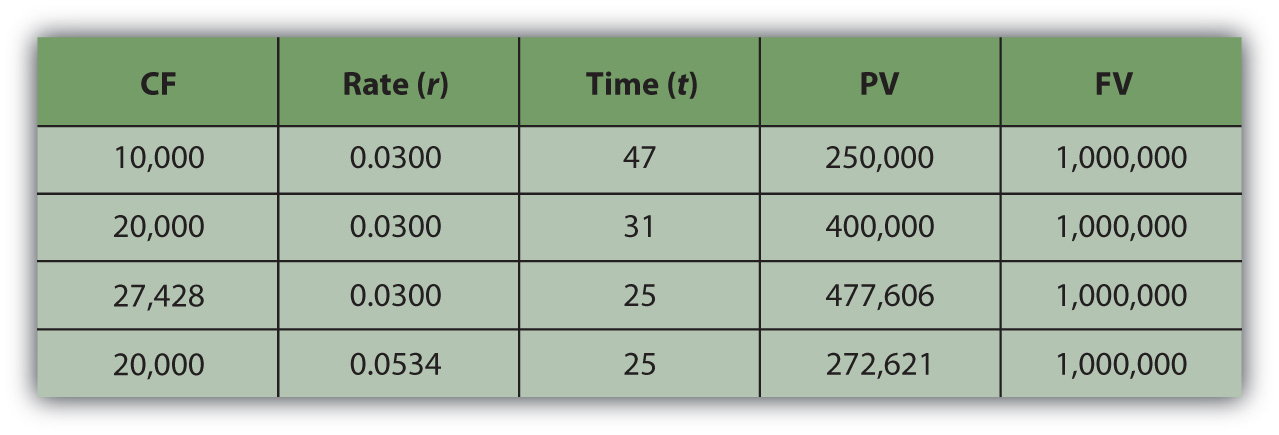
For example, if you desire to have $1,000,000 (FV) in the bank when yous retire, and your bank pays three percent (r) interest per year, and you can save $10,000 per yr (CF) toward retirement, can y'all afford to retire at historic period sixty-v? You could if you start saving at age eighteen, considering with that almanac saving at that rate of return, it will take twoscore-seven years (t) to have $1,000,000 (FV). If you could relieve $20,000 per year (CF), it would merely take 30-one years (t) to relieve $1,000,000 (FV). If yous are already 40 years old, you could do it if you save $27,428 per year (CF) or if y'all can earn a return of at to the lowest degree 5.34 percent (r) (Effigy 4.12 "Retirement Savings Calculations").

Figure four.12 Retirement Savings Calculations

As you can see, the relationships between time, risk, opportunity cost, and value are some of the nearly important relationships y'all volition ever encounter in life, and understanding them is critical to making audio financial decisions.

Financial Calculations

Modern tools brand information technology much easier to practice the math. Calculators, spreadsheets, and software accept been developed to be very user friendly and widely bachelor.

Fiscal calculators are designed for financial calculations and take the equations relating the present and future values, cash flows, the disbelieve rate, and time embedded, for single amounts or for a series of cash flows, so that you can summate any i of those variables if you know all the others.

Personal finance software packages usually come with a planning calculator, which is nothing more than a formula with these equations embedded, and so that you can find any one variable if you know the others. These tools are usually presented as a "mortgage calculator" or a "loan calculator" or a "retirement planner" and are ready to answer common planning questions such every bit "How much do I have to relieve every year for retirement?" or "What will my monthly loan payment be?"

Spreadsheets also have the equations already designed and readily accessible, equally functions or as macros. There are also stand up-alone software applications that may be downloaded to a mobile device, such every bit a smartphone or Personal Digital Assistant (PDA). They are useful in answering planning questions merely lack the ability to shop and rail your situation in the way that a more complete software package tin can.

The calculations are discussed hither non and then that you tin perform them, as you take many tools to cull from that can do that more than efficiently, just so that you can empathize them, and most importantly, so that you lot tin can empathise the relationships that they describe.

Key Takeaways

• The thought of the time value of coin is fundamental to financial decisions.
• The present value of the series of cash flows is equal to the sum of the nowadays value of each cash flow.
• A series of cash flows is an annuity when there are regular payments at regular intervals and each payment is the same amount.

• To calculate the present value of an annuity, you need to know

  • the amount of the identical cash flows (CF),
  • the frequency of the cash flows,
  • the number of greenbacks flows (t),
  • the discount rate (r) or the rate at which fourth dimension affects value.

• The adding for the present value of an annuity yields valuable insights.

  • The more than time (t), the more periods and the more than periodic payments, that is, the more than cash flows, and so the more liquidity and the more than value.
  • The greater the greenbacks flows, the more than liquidity and the more value.
  • The greater the rate at which time affects value (r) or the greater the opportunity toll and risk or the greater the charge per unit of discounting, the more than time affects value.

• The calculation for the hereafter value of an annuity yields valuable insights.

  • The more time (t), the more than periods and the more than periodic payments, that is, the more greenbacks flows, and so the more than liquidity and the more than value.
  • The greater the cash flows, the more liquidity and the more value.
  • The greater the rate at which time affects value (r) or the greater the rate of compounding, the more than time affects value.
• A perpetuity is an space annuity.

Exercises

1. In My Notes or in your financial planning journal, identify and record all your cash flows. Which cash flows function every bit annuities or perpetuities? Summate the nowadays value of each. And so summate the futurity value. Which cash flows requite you lot the greatest liquidity or value?
2. How tin can you determine if a lump-sum payment or an annuity volition have greater value for you?
3. Survey and sample financial calculators listed at http://world wide web.dinkytown.net/, http://world wide web.helpmefinancial.com/, and http://world wide web.financialcalculators.com. Which ones might prove especially useful to you? What do you place every bit the principal strengths and weaknesses of using fiscal calculators?

johnsoncoursentand.blogspot.com

Source: https://saylordotorg.github.io/text_personal-finance/s08-03-valuing-a-series-of-cash-flows.html

Share this post